|
Plane and Circularly
Polarized EM Waves(平面圆极EM波)
Electromagnetic waves are
transverse in the sense that associated electric and magnetic
field vectors are both perpendicualr to the direction of wave
propagation. The Poynting vector defined by
S = E x H (W/m^2),
indicates not only the magnitude
of the energy flux density (energy flow rate per unit area per
unit time, Watts/m^2) but also the direction of energy flow. For
simple electromagnetic waves, the Poynting vector is in the same
direction as the wavevector, k.
The first animation shows propagation of sinusoidal plane
electromagnetic waves in the z direction. The electric field is
assumed in the x direction, and the magnetic field in the y
direction.
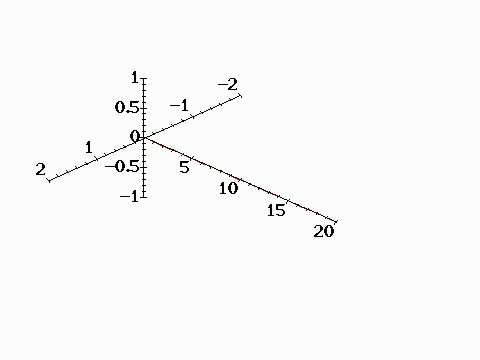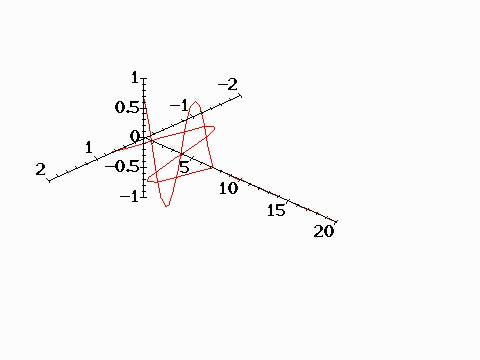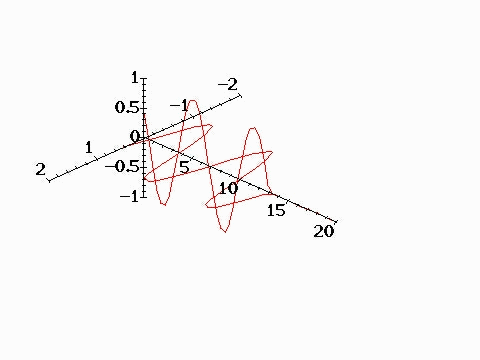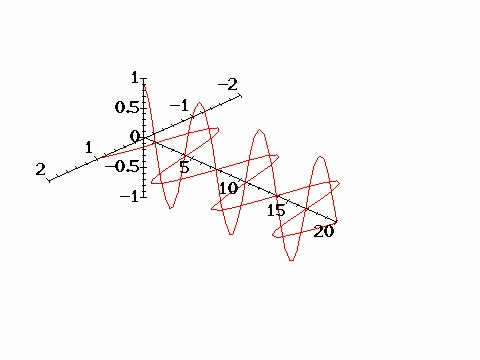
A plane electromagnetic wave can
be considered as vector combination of two circularly polarized
waves rotating in opposite directions. The animation below shows
propagation of electric field associated with a circularly
polarized wave with postitive helicity. (Positive helicity is
the case such that a screw would move in the direction of wave
propagation if rotated with the electric field. In optics, it is
called "left hand" circualr polarization. Negative helicity
(right hand polarization) refers to rotation in the oppsite
direction.) The moving end of the helix indicates the head of
the electric field vector which is rotating about the z axis as
shown in the right figure.

Animation below shows vector sum
of two circularly polarized waves with opposite helicities which
results in formation of a plane wave. Electromagnetic waves
emitted by charged particles undergoing circualr motion (e.g.,
electrons trapped in a magnetic field) are in general circularly
(or elliptically) polarized. Circularly polarized waves carry
angular momentum as well as energy and momentum. The angular
mometum flux density is given by
R = r x (E x H)/c,
as discussed in Example 6, p. 161
of the textbook.
图1+图2=图3
图3
To repeat animation, click "Back" then
"Forward" buttons. |