|
Dispersive Waves(色散波)
In a nondispersive wave medium, waves can propagate without
deformation Electromagnetic waves in unbounded free space are
nondispersive as well as nondissipative and thus can propagate
over astronomical distances. Sound waves in air are also nearly
nondispersive even in the ultrasonic frequency range. If not,
that is, if high frequency notes (e.g., piccolo) and low
frequency notes (e.g., base) propagate at different velocities,
they would reach our ears at different times, and music played
by an orchestra would not be harmonious. Most waves in material
media are dispersive, however, and wave forms originally set up
are bound to change in a manner that the wave energy is more
spatially spread out or dispersed.
Animation 1 below shows propagation of dispersive wave
packet and Animation 2 nondispersive wavepacket. In making the
animation, 100 sinusoidal waves are superposed for a dispersion
relation,
(The dispersion relation describes the
ion acoustic wave in a plasma and also approximately shallow
water waves. See, for example, A. Hirose et al., Plasma Physics,
Vol. 20, p. 1179 (1978), in which response of the ion acoustic
wave to an impulse has been analyzed.) Note that in the
dispersive case shown in the top animation, long wavelength
components propagate faster than short wavelength components.
The envelope of the wave packet propagates at the group
velocity. Wave ripples propagate at the phase velocity. In
contrast, nondispersive wave packet (Animation 2) described by
maintains the original wave form.
Animation 3 shows superposition of two sinusoidal waves in
dispersive case, sin(x - t) + sin(1.2x - 1.1t) (group velocity =
half of phase velocity), while the last animation shows the case
of nondisperve wave, sin(x - t) + sin(1.2x - 1.2t). Note that in
the dispersive case (Animation 3), wave propagation is not
simple parallel shift.
1. Dispersive wavepacket
> with(plots):
animate(sum(.07*(exp(-(.1*k-3)^2)+exp(-(0.1*k+3)^2))*cos(.1*k*x-.1*k/sqrt(1+.1*(.1*k)^2)*t),k=1..100),x=-4..20,t=0..30,frames=60,numpoints=200,color=red);
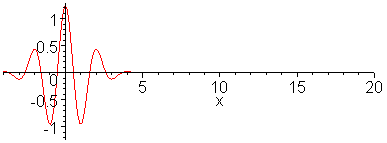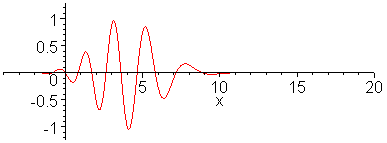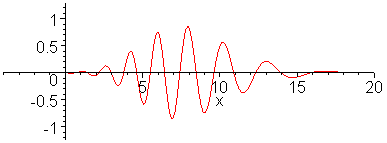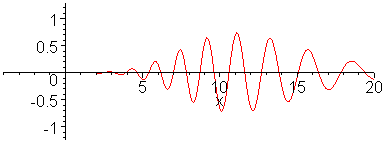
2. Nondispersive wavepacket
>
animate(sum(.07*(exp(-(.1*k-3)^2)+exp(-(0.1*k+3)^2))*cos(.1*k*x-.1*k/sqrt(1+.0*(.1*k)^2)*t),k=1..100),x=-4..20,t=0..30,frames=60,numpoints=200,color=red);
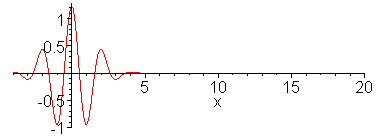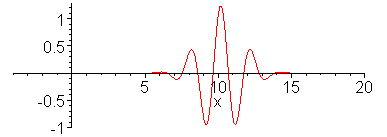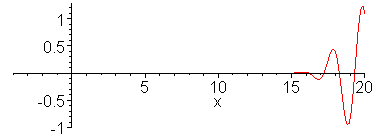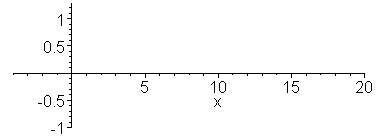
3. Dispersive sinusoidal waves
>
animate(sin(x-t)+sin(1.2*x-1.1*t),x=0..50,t=0..63,numpoints=150,frames=100,color=red);

4. Nondispersive sinusoidal waves
>
animate(sin(x-t)+sin(1.2*x-1.2*t),x=0..50,t=0..63,numpoints=150,frames=100,color=red);

|