Reflection of Electromagnetic Waves(电磁波的反射)

The impedance for electromagnetic waves is defined as the ratio between the voltage and current waves,

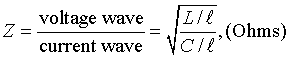
where

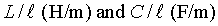
are inductance and capacitance per unit length in medium. For example,the inductance,capacitance, and impedance of a coaxial cable is given by

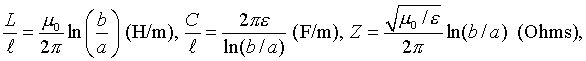
where a and b are the inner and outer radii of the cable, and

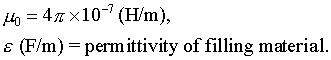
In free space, the impedance is

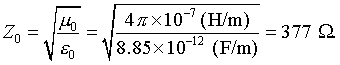
As mechanical waves are reflected at an impedance discontinuity, so are electromagnetic waves. For an incident voltage wave Vi , the reflected voltage wave at an impedance discontinuity is

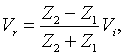
which should be compared with that for mechanical displacement waves,

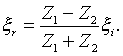
The difference is due to the fact that displacement wave corresponds to current wave, while force wave corresponds to voltage wave. In fact, the current waves obey a formula similar to that of displacement wave,

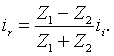
The first and second animation shows,respectively, reflection of voltage and current waves at the end of a 50 Ohm cable terminated with a 25 Ohm resistor. The generator (10 V dc) is assumed to have the same resistance (50 Ohms) as the cable impedance to avoid further reflection. If the generator has zero impedance, multiple reflections take place as shown in the second animation. The case of zero generator impedance is shown in the third and fourth animation.

The fifth animation shows reflection and transmission of sinusoidal waves when the impedance of termianting load is one quarter of the cable impedance.

Reflection can be avoided entirely if a third medium having an impedance and length of quarter wavelength is inserted. This well known quarter wavelength impedance matching is shown in the last animation. Note that there are no standing waves and all wave energy is smoothly transferred to the cable 2.

V_g = 10 V, R_G = 50 Ohms, Z = 50 Ohms, R_L = 25 Ohms

Evolution of the voltage wave.
with(plots):
animate(5*Heaviside(t-x)-5/3*Heaviside(t+x),x=-10..1,t=-9..11,color=red,numpoints=300,frames=100,view=[-10..0,0..5]);

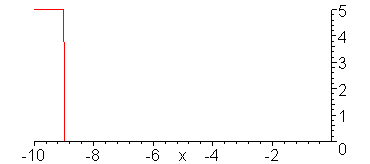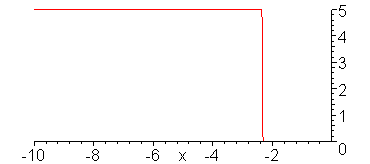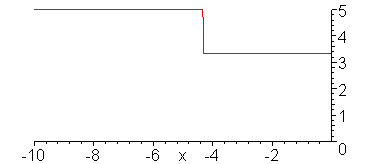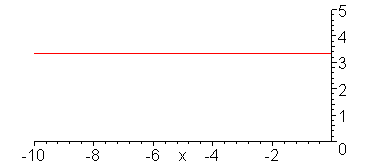
Evolution of the current wave.
animate(.1*Heaviside(t-x)+.1/3*Heaviside(t+x),x=-10..1,t=-9..11,color=red,numpoints=300,frames=100,view=[-10..0,0..0.2]);

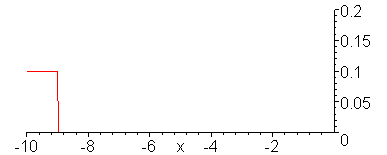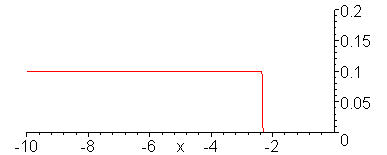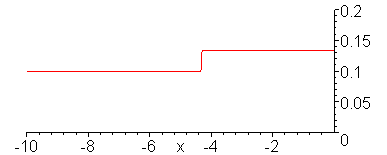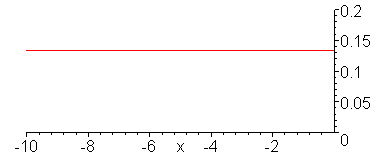
V_g = 10 V, R_G = 0, Z = 50 Ohms, R_L = 25 Ohms
Voltage wave.
animate(10*Heaviside(t-x)-10/3*Heaviside(t+x)+10/3*Heaviside(t-x-10)-10/9*Heaviside(t+x-10)+10/9*Heaviside(t-x-20)-10/27*Heaviside(t+x-20)+10/27*Heaviside(t-x-30),x=-5..0,t=-6..30,color=red,numpoints=300,frames=200,view=[-5..0,0..10]);

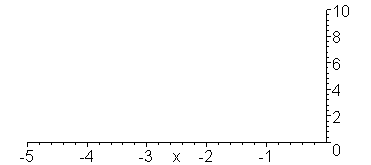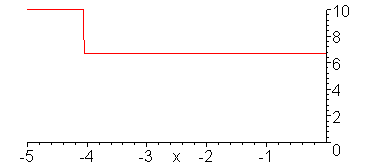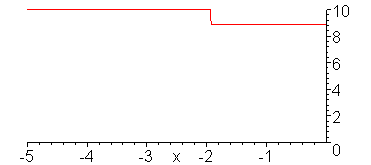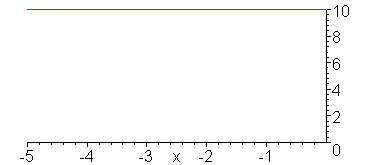
Current wave.
animate(.2*Heaviside(t-x)+.2/3*Heaviside(t+x)+.2/3*Heaviside(t-x-10)+.2/9*Heaviside(t+x-10)+.2/9*Heaviside(t-x-20)+.2/27*Heaviside(t+x-20)+.2/27*Heaviside(t-x-30),x=-5..0,t=-6..30,color=red,numpoints=300,frames=200,view=[-5..0,0..0.4]);

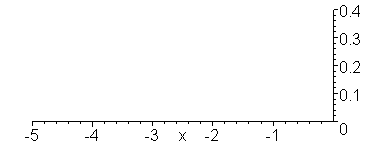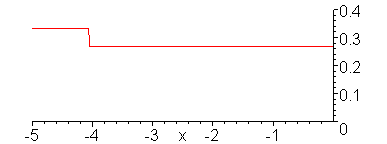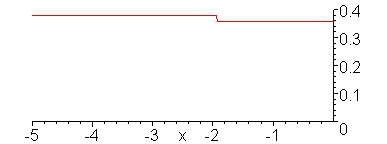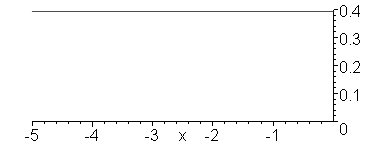
Reflection of sinusoidal voltage wave when V_g = 1 V, Z_2/Z_1 = 1/4. Note formation of incomplete standing in medium 1.
with(plots):
animate((sin(.1*t-x)-3/5*sin(x+.1*t))*Heaviside(-x)+2/5*sin(.1*t-4*x)*Heaviside(x),x=-10..5,t=0..62,frames=30,color=red,numpoints=300);

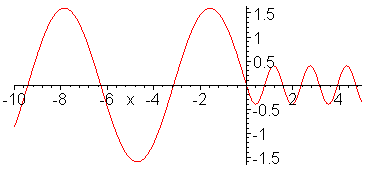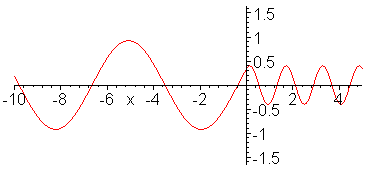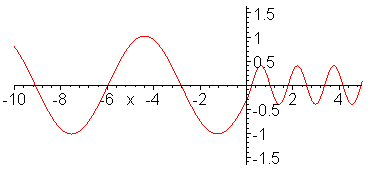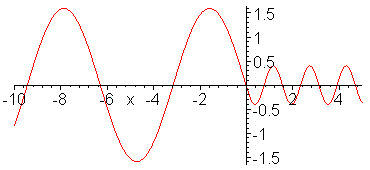
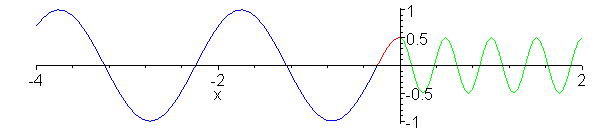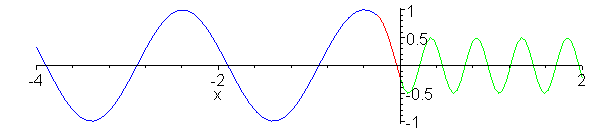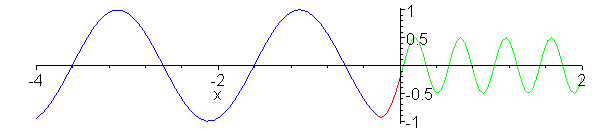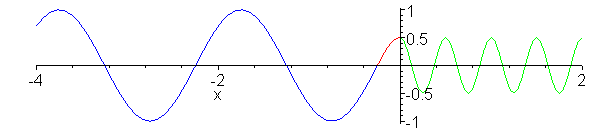
Impedance matching. Z_1 = 1, Z_2 = 1/4, Z_3 = 1/2. Inserted Z_3 medium (shown in red) is quarter wavelength thick (or long). No reflection occurs and wave energy is smoothly transfered to cable 2. Note the absence of standing waves.
with(plots):
a:=animate(.75*(cos(2*Pi*.1*t-2*Pi*x)-1/3*cos(2*Pi*.1*t+2*Pi*x)),x=-0.25..0,t=0..20,color=red,frames=60):
b:=animate(cos(2*Pi*.1*t-2*Pi*x/2+Pi/4),x=-4..-0.25,t=0..20,color=blue,frames=60):
c:=animate(.5*cos(2*Pi*.1*t-4*Pi*x),x=0..2,t=0..20,color=green,frames=60):
display({a,b,c});