Solitons(孤立子)
Waves are in general dispersive and the original
wave form becomes dispersed as waves propagate over a large
distance. However, in some waves, dispersion can be
compensated by nonlinearity and they can propagate over a
large distance keeping original wave forms. Waves in shallow
water and plasma waves known as the ion acoustic wave are
typical examples. In fact both waves can be described by a
common nonlinear wave equation (KdeV equation) originally
derived by Kortweg and de Vries.
Animation shows propagation of large
(amplitude = 8) and small (amplitude = 2) amplitude solitons and
their passing collision. Soliton propagates faster as its
amplitude increases and if two solitons of different amplitudes
are created, collision can occur. Note that collision does not
destroy wave forms of either wave. Snapshots before, at, and
after collision are also shown. At the instant of collision, the
wave amplitude becomes smaller than the sum of the two waves.
This is a typical nonlinear behavior wherein the superposition
principle, which works universally in linear waves, entirely
breaks down. Similar nonlinear wave propagation occurs in light
waves guided along an optical fiber.
Fast, larger amplitude soliton. Amplitude = 8.
> with(plots):
animate(8*(sech(2*(x-.5*16*t)))^2,x=-10..10,t=-1.2..1.2,frames=49,numpoints=500,color=red,view=[-10..10,0..10]);
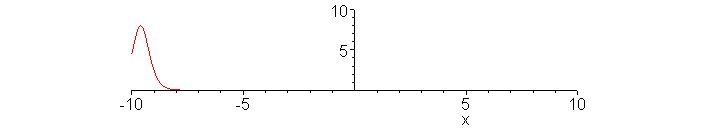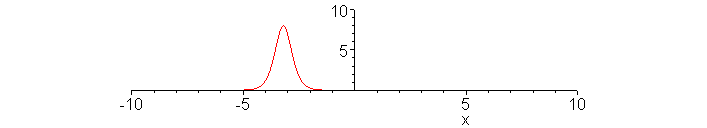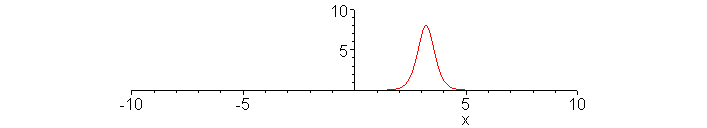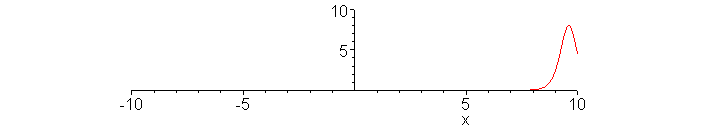
Slow, smaller amplitude soliton. Amplitude =
2. Velocity is one half of that of the fast soliton.
>
animate(2*(sech(x-.5*4*t))^2,x=-10..10,t=-1.2..1.2,frames=49,numpoints=500,color=red,view=[-10..10,0..10]);

Passing collision of fast and slow solitons.
> with(plots):
animate(12*(3+4*cosh(2*x-.5*8*t)+cosh(4*x-.5*64*t))/(3*cosh(x-.5*28*t)+cosh(3*x-.5*36*t))^2,x=-10..10,t=-1.2..1.2,frames=49,numpoints=1000,color=red,view=[-10..10,0..10]);

Snapshot at t = -1.
> t:=-1:
plot(12*(3+4*cosh(2*x-.5*8*t)+cosh(4*x-.5*64*t))/(3*cosh(x-.5*28*t)+cosh(3*x-.5*36*t))^2,x=-10..10,numpoints=1000,color=red,view=[-10..10,0..10]);

Snapshot at t = -0.5.> t:=-0.5:
plot(12*(3+4*cosh(2*x-.5*8*t)+cosh(4*x-.5*64*t))/(3*cosh(x-.5*28*t)+cosh(3*x-.5*36*t))^2,x=-10..10,numpoints=1000,color=red,view=[-10..10,0..10]);

Snapshot at t = 0. Note that the amplitude is
only 6.0. The pulse width is broadened.
> t:=0:
plot(12*(3+4*cosh(2*x-.5*8*t)+cosh(4*x-.5*64*t))/(3*cosh(x-.5*28*t)+cosh(3*x-.5*36*t))^2,x=-10..10,numpoints=1000,color=red,view=[-10..10,0..10]);

Snapshot at t = 0.5.
> t:=0.5:
plot(12*(3+4*cosh(2*x-.5*8*t)+cosh(4*x-.5*64*t))/(3*cosh(x-.5*28*t)+cosh(3*x-.5*36*t))^2,x=-10..10,numpoints=1000,color=red,view=[-10..10,0..10]);

Snapshot at t =1.> t:=1.0:
plot(12*(3+4*cosh(2*x-.5*8*t)+cosh(4*x-.5*64*t))/(3*cosh(x-.5*28*t)+cosh(3*x-.5*36*t))^2,x=-10..10,numpoints=1000,color=red,view=[-10..10,0..10]);
 |